VLNY

Na této stránce naleznete:
	Základní vztahy
	Základní jevy

 

Základní vztahy
ψ(t, x) = A(t,x) exp[i φ(t, x)]	Vlnová funkce. Komplexní funkce popisující libovolné vlnění (ψ může být libovolná veličina − teplota, hustota, výchylka, elektrické pole, tlak, ...
A(t, x)	Amplituda vlnění, reálná funkce.
φ(t, x)	Fáze vlnění, reálná funkce.
ω ≡ ∂φ/∂ t	Úhlová frekvence. Pro periodické děje v čase je ω = 2π/T.
k ≡ ∂φ/∂ x	Vlnový vektor. Pro periodické děje v prostoru je k = 2π/λ.
vf = ω/k	Fázová rychlost. Rychlost šíření fáze (přemisťování oblasti bodů se shodnou fází). Nemá nic společného se skutečným pohybem bodů (kola na vodě × pohyb částic vody). Může být i nadsvětelná. Nadsvětelné rychlosti často vznikají jen různými geometrickými efekty. Prohlédněte si příklady "Prasátko" a "Kvasary".
vg = ∂ω/∂k	Grupová rychlost. Rychlost přenášení energie (skutečného pohybu částic). Musí být vždy podsvětelná. Prohlédněte si příklad "Disperzní relace".
ψ(t, x) = A0 exp[i (kx − ωt)]	Rovinná vlna. Nejjednodušší vlnoplocha. Plochy konstantní fáze jsou roviny přesouvající se rychlostí ω/k.
ψ(t, r) = (K/r) exp[i (kr − ωt)]	Kulová vlna. Vzniká například při šíření vzruchu od exploze v homogenním prostředí.Amplituda ubývá jako 1/r, hustota energie jako 1/r2. Prohléděte si příklad "Detonační vlna".
ψ(t, r) = (K/r1/2) exp[i (kr − ωt)]	Kruhová vlna. Například kola na vodní hladině. Amplituda ubývá jako 1/r1/2, energie jako 1/r. Prohlédněte si příklad "Podélná vlna v davu".
α1 = α2	Zákon odrazu.
sin α1 / sin α2 = v1/v2	Snellův zákon lomu.
ω  = ω0 (1 ± v/c)	Dopplerův jev. Nerelativistický pohyb pozorovatele.
ω  = ω0 / (1 ± u/c)	Dopplerův jev. Nerelativistický pohyb zdroje. Vzhledem k tomu, že u/c << 1, můžeme koreci k frekvenci psát stejně tak dobře v čitateli i ve jmenovateli.
sin α/2 = c/u	Rázová vlna. Je-li rychlost zdroje u je větší než rychlost šíření vlny c, vzniká rázová vlna s vrcholovým úhlem α.
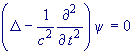	Vlnová rovnice. Základní rovnice, kterou splňuje široká třída vlnění.
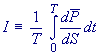	Intenzita vlnění. Střední časová hodnota výkonu na jednotkovou plochu [W/m2].
L ≡ 10 log (I /I0)	Hladina intenzity. Intenzita v logaritmické míře [dB]. Zpravidla I0 = 10−12 W/m2. Prohlédněte si příklad "Hluk".
Základní jevy
Huyghensův princip	Každý bod vlnoplochy se stává zdrojem elementárního vlnění. Výslednou vlnoplochou je obálka elementárních vlnoploch ve směru šíření. V opačném směru se vlnoplochy vyruší (Kirchhoff − 19. století).
Fermatův princip	Světelný paprsek se mezi dvěma body šíří po časově nejkratší trajektorii. V přírodě se může realizovat i trajektorie která má v závislosti na čase maximum nebo inflexní bod.
Dopplerův jev	Přibližuje-li se zdroj vlnění a pozorovatel, dochází k zvýšení pozorované frekvence. Vzdaluje-li se zdroj vlnění a pozorovatel, dochází k snížení pozorované frekvence. Prohlédněte si příklady "Ladička" a "Rotující hvězda".
Disperzní relace, disperze	Disperzní relace je vztah mezi úhlovou frekvencí a vlnovým vektorem. Pro rovinné monochromatické vlny má tvar ω = ck, pro složitější vlnění může být disperzní relace značně komplikovaná. Z disperzní relace lze určit fázovou a grupovou rychlost vlnění a závislosti těchto rychlostí na vlnovém vektoru, respektive vlnové délce. Tuto závislost nazýváme disperzí. Prohlédněte si příklad "Disperzní relace".