RELATIVITA - PŘÍKLADY

Na této stránce naleznete:
	Mion
	Interval
	Parametry rychlé částice
	Slunce
	Dopplerův jev
	Heavisideovo pole (ke zkoušce)
	Pound Rebkův experiment
	Kosmologický posuv
	Náboj v elektrickém poli

 

Př. 1.: Mion

• Zadání: Doba života mionu (těžký elektron) je Δτ = 2.2×10⁻⁶ s. Mion vznikl ve výšce h = 30 km nad povrchem Země z kosmického záření a dopadl na Zem. Jakou musel mít minimální  rychlost při vzniku?

• Řešení: Z hlediska pozorovatele na Zemi je mion v pohyblivé soustavě a doba jeho života se prodlužuje na Δt = γΔτ. Mion proto může ulétnout až vzdálenost h ≤ υΔt = υγΔτ. Z tohoto vztahu vypočteme rychlost, kterou musí minimálně mít: υ = c/[1 + (cΔτ/h)²]^1/2.
• Výsledek: υ = 0.99976 c

Př.2.: Interval

• Zadání: Dokažte, že interval Δs² = − c²Δt² + Δx² + Δy² + Δz² je invariantní, tj. nezávisí na volbě souřadnic.
• Předpoklady: Předpokládáme, že máme dvě události (t_a, x_a, y_a, z_a) a (t_b, x_b, y_b, z_b) a v nějaké soustavě vypočteme veličinu   Δs², kde Δt = t_b − t_a, Δx = x_b − x_a, ... Tato veličina rozhoduje o tom, zda události mohou být kauzálně svázané a musí vyjít ve všech souřadnicových soustavách stejně.

• Řešení: Vyjdeme z Lorentzovy transformace

V čárkované soustavě pro interval obou událostí máme:

Δs' ² =  − c²Δt' ² + Δx' ² + Δy' ² + Δz' ² =  
= − c²γ² (Δt − vΔx/c²)² + γ² (Δx − vΔt)² + Δy² + Δz² =  
= − c²γ²(1 − v²/c²)Δt² + γ²(1 − v²/c²)Δx² + Δy² + Δz² =  
= − c²Δt² + Δx² + Δy² + Δz² .

Výsledek je tedy shodný v obou soustavách.

Př. 3.: Parametry rychlé částice

• Zadání: Elektron je urychlen napětím U = 10⁶ V. Určete jeho rychlost z klasického i relativistického výrazu pro kinetickou energii.

• Řešení: Elektron v každém případě urychlením získá kinetickou energii W_k = QU. V klasickém případě je

W_k = m₀υ²/2    →    υ = (2W_k/m₀)^1/2 = (2QU/m₀)^1/2.

V relativistickém případě je

W_k = γm₀c² − m₀c²    →    υ = c[1 − (1 + QU/m₀c²)⁻²]^1/2.

• Výsledek: υ_nerel = 1.98 c, υ_rel = 0.94 c. Nerelativistický výraz tedy zjevně nemůžeme v tomto případě použít, vede k nadsvětelným rychlostem.

Př. 4.: Slunce

• Zadání: Jak se změní hmotnost Slunce za jeden rok díky jeho vyzařování? Intenzita slunečního záření v okolí Země je I = 1.4 kW m⁻².

• Řešení: Δm = ΔE/c² = PΔt /c² = 4πR²I Δt/c².
• Výsledek: Δm ~ 10¹⁷ kg. Celková hmotnost Slunce je 2×10³⁰ kg. Jde tedy o zanedbatelný zlomek.

Př. 5.: Dopplerův jev

• Zadání: Odvoďte relativistický Dopplerův jev pomocí transformace čtyřvektoru (ω/c, k). Proč dochází k Dopplerovu jevu i tehdy, když zdroj pozorovatele jen míjí a jejich vzdálenost se nemění (tzv. transverzální Dopplerův jev)?
• Řešení:

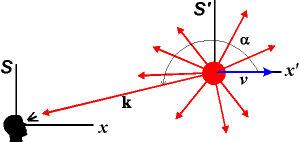
Snadno nalezneme řešení v soustavě S ' spojené s zdrojem záření:
k_μ = (ω₀/c; k_xcos α; k_ysin α; 0) = (ω₀/c; ω₀/c cos α; ω₀/c sin α; 0). Nyní provedeme Lorentzovu transformaci do soustavy pozorovatele S:

.

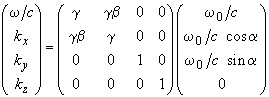Z prvního řádku maticového násobení máme výsledek

ω = γ (1 + v/c cos α) ω₀.

tento vztah je známý jako relativistický Dopplerův jev. V limitě nízkých rychlostí (zanedbáme členy kvadratické a vyšší v v/c) je c → 1 a ω = (1 + v/c cos α) ω₀. Při vzdalování zdroje je α = 180° a ω = (1 − v/c) ω₀, při přibližování zdroje je α = 0° a ω = (1 + v/c) ω₀. Jde o známé nerelativistické Dopplerovy vztahy. Při vyšších rychlostech jsou tyto vztahy modifikovány koeficientem γ. Jestliže zdroj záření pozorovatele míjí (α = ± 90°) je ω = γ ω₀. K změně frekvence tedy dochází i v případě, že se zdroj nevzdaluje ani nepřibližuje. Tento jev se nazývá transverzální Dopplerův jev a jde o čistě relativistický jev, který nemá v nerelativistické fyzice obdoby. Je způsoben změnou chodu času v pohybující se soustavě.

Př. 6.: Heavisideovo pole (ke zkoušce)

• Zadání: Určete pole náboje letícího konstantní rychlostí. Využijte transformaci čtyřvektoru (Φ/c, A).
• Řešení:

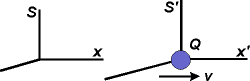
Provedeme transformaci do soustavy S pozorovatele

.  

Výsledek je

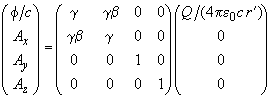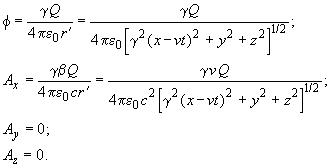
Je zřejmé, že magnetické pole B = rot A je již nenulové, a že elektrické pole E = − ∂A/∂t − ∂Φ/∂x je také modifikováno. Nový tvar polí je

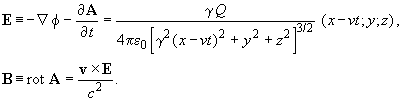
Důležitá je kolmá a rovnoběžná složka elektrického pole:

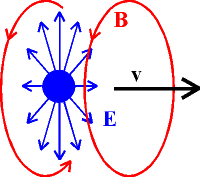
Vidíme, že elektrické pole ve směru pohybu je stlačeno faktorem γ⁻² a napříč pohybu je nataženo faktorem γ. Pole se pohybuje spolu s nábojem. Magnetické pole tvoří kružnice kolmé na pohyb náboje. Pro nekonečnou řadu nábojů bychom získali pole kolem vodiče. Podobně lze postupovat při transformaci energie a hybnosti, hustoty a proudové hustoty, atd. Prohlédněte si aplet "Heavisideovo pole".

Př. 7.: Pound Rebkův experiment

• Zadání: Určete relativní změnu frekvence a vlnové délky v Pound-Rebkově experimentu. Foton prolétal starou vodárenskou věží o výšce Δh = 22.6 m. Použity byly fotony s energií 14.4 keV emitované izotopem železa Fe57.
• Řešení: Ze vztahu Δω/ω₀ = − Δλ/λ₀ = ΔΦ/c²  = gΔh/c² snadno určíme Δω/ω₀ = 2.5×10 ⁻¹⁵, Δλ/λ₀ = − 2.5×10 ⁻¹⁵.

Př. 8.: Kosmologický posuv

• Zadání: Quasar má rudý posuv z = 2.5. Určete pozorovanou vlnovou délku čáry λ = 680 nm. Jaké byly rozměry Vesmíru v době, kdy quasar vyslal záření?

• Řešení: Stačí vyjít ze základního vztahu pro kosmologický rudý posuv: z = Δλ/λ₀ = [R(t) − R(t₀)]/R(t₀). Odsud snadno určíme:

2.5 = λ/λ₀ − 1    →    λ = 3.5 λ₀ = 2380 nm.

Obdobně

2.5 = R/R₀ − 1    →    R₀ = R /3.5 = 29% R.

Vlnová délka je posunuta do neviditelné infračervené oblasti spektra. Rozměry Vesmíru byly v době vyslání signálu 29% rozměrů dnešních.

Př. 9.: Náboj v elektrickém poli

Zadání: Řešte urychlování náboje z nulové rychlosti ve směru pole nerelativisticky a relativisticky.
Řešení nerelativistické: Budeme integrovat pohybovou rovnici

.

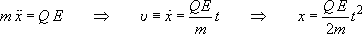Nerelativistické řešení má zjevné vady, například 

 .

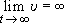Náboj je nekontrolovatelně urychlován na jakoukoli rychlost.
Řešení relativistické: Budeme integrovat relativistickou pohybovou rovnici

 .

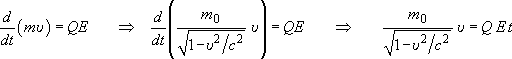Vidíme, že po první integraci jsme nedostali rychlost samotnou, ale vztah, ze kterého teprve musíme rychlost vypočítat:

 .

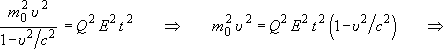
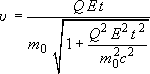Výraz pro rychlost již není tak jednoduchý, zato ale nediverguje, 

 .

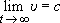Chcete-li znát polohu, je třeba provést ještě jednu integraci:

 .
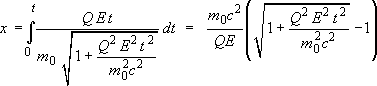
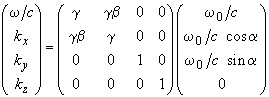
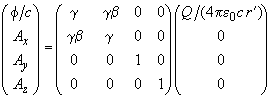
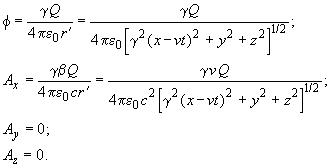
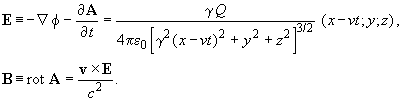
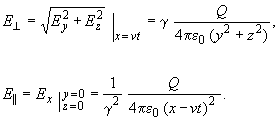
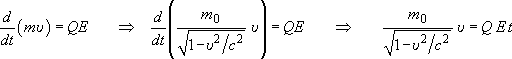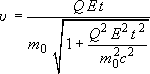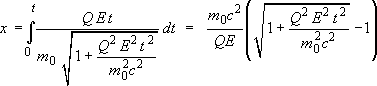