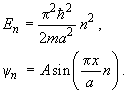|
 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
KVANTOVÁ TEORIE - PŘÍKLADY
Př. 1.: Stefan Boltzmannův zákon
Př. 2.: Wiennův zákon
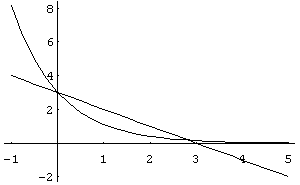
a získáme transcendentní rovnici (3 − x) = 3 exp(−x). Tato
rovnice může být snadno řešena numericky nebo graficky (v grafu najdeme
průsečík funkcí na levé a pravé straně rovnice). Řešení rovnice je buď
Př. 3.: Slunce
T = [IZRZS2/σRS2]1/4.
T = b/λmax .
Př. 4.: Člověk
λmax = b/T = 0.00289/310 m = 9.3×10−6 m.
Př. 5.: Čára Hα
ΔE = E3 − E2 = E1/9 − E1/4 = −13,6 eV (1/9 − 1/4) = 1.88 eV.
Př. 6.: Mikroskop
Př. 7.: Komutátor (ke zkoušce)
[x, d/dx] f = (x d/dx − d/dx x) f = x df/dx − d/dx (xf ) = x df/dx − f − x df/dx = − f .
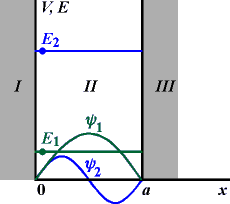
[x, d/dx] = −1. Př. 8.: Jáma
ψ = A sin kx + B cos kx .
B = 0 , k = πn/a , n = 1, 2, 3, ... .
Př. 9.: Emise
|
||||||||||||||||||||||||||||||||||||||||||||||||
 |
|
 |
||||||||||||||||||||||||||||||||||||||||||||||
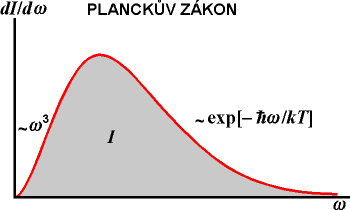
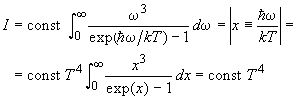 .
.
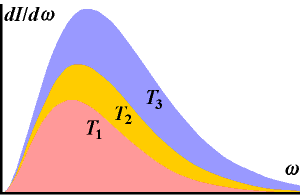
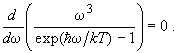

 Zadání: Nalezněte vlnovou délku na které vyzařuje maximum energie
člověk o teplotě 37 °C.
Zadání: Nalezněte vlnovou délku na které vyzařuje maximum energie
člověk o teplotě 37 °C.