ELEKTROMAGNETICKÉ VLNY

Na této stránce naleznete:
	Matematické vztahy
	Některé vektorové identity
	Pravidla pro FT
	Maxwellovy rovnice pro pole
	Maxwellovy rovnice pro potenciály
	Základní vztahy z elmg. teorie
	Vlna na rozhraní

Matematické vztahy
f: R3(R4) → R	Skalární pole. Poloze (času a poloze) přiřadíme reálnou hodnotu (teplotu, hustotu, výchylku, tlak, energii, ...). Například: p = p(x, y, z), resp. p = p(t, x, y, z).
K: R3(R4) → R3	Vektorové pole. Poloze (času a poloze) přiřadíme vektor (rychlost., elektrické pole, magnetické pole, ...). Například: B = B(x, y, z), resp. B = B(t, x, y, z).
γ, S, V	Křivka, plocha, objem.
∂γ, ∂S, ∂V	Hranice křivky, plochy, objemu.
dl = (dx, dy, dz)	Vektorový délkový element.
dl = (dx2 + dy2 + dz2)1/2	Skalární délkový element.
dS = n dS	Vektorový plošný element. Vektor normály n míří u uzavřené plochy směrem ven.
dS	Skalární plošný element.
dV	Objemový element
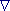≡ (∂/∂x, ∂/∂y, ∂/∂z)	Operátor "Nabla". Parciální derivace podle jednotlivých proměnných. Také gradient či ∂/∂x.
grad f ≡ 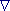 f ≡ (∂f/∂x ; ∂f/∂y ; ∂f/∂z)	Gradient funkce. Vektor kolmý k plochám konstantních hodnot funkce f, míří k maximu funkce. Prohlédněte si příklad "Gradient".
rot 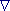K ≡ ×K ≡  (Kz , y− Ky,z ; Kx,z− Kz,x ; Ky,x− Kx, y)	Rotace vektorové funkce. Rotace je nenulová jen v centrech vírů vektorové funkce. Lze pomocí ní snadno zapsat cirkulaci vektorové veličiny. Zápisy typu Kx, y znamenají zkratku pro ∂Kx/∂y. Rotace je opět uspořádanou trojicí čísel. Prohlédněte si příklad "Rotace".
div 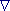K ≡ ·K ≡  (Kx,x + Ky,y  + Kz,z)	Divergence vektorové funkce. Divergence je nenulová jen v zdrojích a propadlech vektorové funkce. Lze pomocí ní snadno zapsat tok vektorové veličiny plochou. Divergence je skalár, tj. jedno jediné číslo. Prohlédněte si příklad "Divergence".
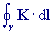	Cirkulace pole K. Křivkový integrál druhého druhu podél uzavřené křivky γ.
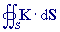	Tok pole K. Plošný integrál druhého druhu přes uzavřenou plochu S.
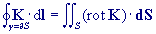	Stokesova věta. Převod cirkulace pole po uzavřené křivce (křivkového integrálu) na plošný integrál.
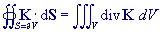	Gauss-Green-Ostrogradského věta. Převod toku pole přes uzavřenou plochu na objemový integrál.
Některé vektorové identity
div rot K = 0	Lze dokázat: div P = 0 K : P = rot K.
rot grad f = 0	Lze dokázat: rot P = 0 Φ: P = − grad Φ.
rot rot K = grad div K − ΔK	"Matfyzácký pokřik"
div (A×B) = B rot A − A rot B
A×(B×C) = B(A·C) − C(A·B)	BÁC−CÁB pravidlo.
Pravidla pro Fourierovu transformaci Předpokládáme konvenci F(t, x) = ∫G(ω, k) exp[i(k·x − ωt)] dωd3k.
∂/∂t → − i ω	grad → + i k
∂/∂x → + i kx	div → + i k·
∂/∂y → + i ky	rot → + i k×
∂/∂z → + i kz	Δ → − k2
Prohlédněte si příklady "Vlny ve vakuu", "Vlny v anisotropním prostředí", "Vlny ve vodiči" a "Vlny ve vlnovodu".     Maxwellovy rovnice pro pole
rot E = − ∂B/∂t	Faradayův indukční zákon. Víry elektrického pole vznikají tam, kde se magnetické pole mění s časem. Trojice rovnic pro časový vývoj magnetického pole.
rot H = j + ∂D/∂t	Ampérův zákon. Víry magnetického pole vznikají tam, kde teče elektrický proud, nebo tam, kde se mění elektrické pole s časem. Trojice rovnic pro časový vývoj elektrického pole. Druhý člen na pravé straně se někdy nazývá "Maxwellův posuvný proud".
div B = 0	Gaussova věta magnetostatiky. Magnetické pole nemá žádné zdroje. Neexistuje magnetický monopól. Okrajová podmínka k Faradayovu indukčnímu zákonu.
div D = ρ	Gaussova věta elektrostatiky. Zdrojem elektrických polí jsou elektrické náboje. Okrajová podmínka k Ampérovu zákonu
D ≡ ε0E + P = D(E)	Materiálový vztah. Charakterizuje reakce materiálu na přítomnost elektrických polí.
H ≡ B/μ0 − M = H(B)	Materiálový vztah. Charakterizuje reakce materiálu na přítomnost magnetických polí.
ρ	Hustota náboje.
j	Proudová hustota.
Maxwellovy rovnice pro potenciály
(Δ − εμ∂2/∂t2) Φ = − ρ/ε	Rovnice pro skalární potenciál.
(Δ − εμ∂2/∂t2 ) A = − μ j	Rovnice pro vektorový potenciál.
div A +  εμ∂Φ/∂t = 0	Lorentzova podmínka.
B = rot A	Magnetická indukce. Vyjádření z potenciálů pole. Prohlédněte si příklad "Potenciály".
E = − 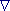Φ − ∂A/∂t	Intenzita elektrického pole. Vyjádření z potenciálů pole.
Hustota náboje a proudová hustota jsou zdrojovými členy Maxwellových rovnic. Známe-li prostorové rozložení nábojů a jejich pohyby, můžeme z Maxwellových rovnic dopočíst vzniklá elektrická a magnetická pole. Tato pole samozřejmě způsobí změny hustoty náboje a proudové hustoty, které lze určit z Lorentzovy pohybové rovnice. Maxwellovy rovnice tak řeší problém odezvy polí na částice, Lorentzova pohybová rovnice odezvu částic na přítomnost polí. Sada posledních pěti rovnic je ekvivalentní Maxwellovým rovnicím. Z rozložení a pohybu nábojů známe hustotu náboje a proudovou hustotu. Z rovnic pro skalární a vektorový potenciál nalezneme veličiny Φ a A splňující Lorentzovu podmínku. Z posledních dvou rovnic potom určíme hodnoty polí. Postup tedy je:  (ρ, j)(Φ, A)(E, B).    Základní vztahy z elektromagnetické teorie
∂ρ/∂t + div j = 0	Rovnice kontinuity. Zákon zachování elektromagnetického náboje.
∂ρW/∂t + div jW = − j·E	Rovnice kontinuity pro energii. Zákon zachování energie elektromagnetického pole. Energie se nezachovává. Napravo stojí hustota Jouleova výkonu. Touto cestou ztrácí elektromagnetické pole energii ve prospěch částic.
ρW =  E·D/2 + H·B/2	Hustota energie. [J/m3]
jW = S ≡ E×H	Tok energie (Poyntingův vektor). [J s−1 m−2]
I = |S| = |E×H|	Intenzita elektromagnetického vlnění. [J s−1 m−2]
I = EH	Intenzita elektromagnetického vlnění v homogenním isotropním prostředí. Prohlédněte si příklad "Sluneční světlo".
c = (εμ)−1/2	Rychlost šíření elektromagnetické vlny.
c = E/B	Vztah mezi elektrickou a magnetickou složkou v elmg vlně. (homogenní, isotropní prostředí).
(Δ − εμ∂2/∂t2 − γμ∂/∂t ) E = 0	Telegrafní rovnice pro elektrické pole.
(Δ − εμ∂2/∂t2 − γμ∂/∂t ) B = 0	Telegrafní rovnice pro magnetické pole. Telegrafní rovnice popisují elektromagnetická pole ve vodičích. Člen s první časovou derivací způsobuje útlum elektromagnetického vlnění ve vodiči. Je-li vodivost nulová (γ = 0), dostáváme z telegrafní rovnice standardní vlnovou rovnici. Prohlédněte si příklad  "Vlny ve vodiči".
Vlna na rozhraní
Et = const	Tečná složka intenzity elektrického pole je na rozhraní konstantní.
Ht ≡ Bt /μ0 − Mt = const	Tečná složka intenzity magnetického pole je na rozhraní konstantní. Rozhraním nesmí téct plošné proudy. Magnetizace M je hustota magnetického dipólového momentu.
Bn = const	Normálová složka magnetické indukce je na rozhraní konstantní.
Dn ≡ ε0En + Pn = const	Normálová složka elektrické indukce je na rozhraní konstantní. Na rozhraní nesmí být plošná hustota náboje. Polarizace P je hustota elektrického dipólového momentu.
ωI = ωR = ωT	Úhlová frekvence dopadající, odražené a lámané vlny je stejná.
α = α'	Zákon odrazu.
sinα/sinβ = vα /vβ ≡ n	Zákon lomu.
sin αm = n	Totální reflexe. Pro úhly dopadu větší než mezní úhel αm dochází k totální reflexi. Aby rovnice měla řešení, musí být n = vα/vβ < 1, tj jde o odraz na opticky řidším prostředí.
tg αB = n	Brewsterův zákon. Je-li úhel dopadu roven Brewsterově úhlu αB, bude odražená vlna obsahovat jen TE mod, tj. bude lineárně polarizovaná. Malá účinnost získávání polarizovaného světla (u skla cca 20 %).
n > 1φ = φ + π	Při odrazu na opticky hustším prostředí dochází k obrácení fáze elektromagnetické vlny.